1. 问题引入

    回归分析是一种预测性建模技术，主要用来研究因变量$y_i$和自变量$x_i$之间的关系，通常被用于预测分析、时间序列等。

    假设特征和结果满足线性关系，则线性回归的目标就是用一条直线去拟合样本点，当新的样本数据进来时，根据拟合的直线去预测新样本的结果。

2. 线性回归模型

2.1 模型建立

    假设南京的房价与房屋的特征满足线性回归模型，我们用$x(1),x(2),…x(N)$表示影响房子价格的特征因素，如面积、房子朝向、地理位置等，房子价格为$h(x)$，是一个由变量$x_i$共同决定的函数，由于不同的因素对房屋价格的影响程度是不同的，所以给每项特征因素赋予一个权重$w(j)$，则得到因变量与自变量之间的函数表达式：

$$h\left ( x \right ) =w_{1}x^{\left ( 1 \right ) } +w_{2}x^{\left ( 2 \right ) }+...+w_{N}x^{\left ( N \right ) } + b$$

写成矩阵的形式，即向量$w=\left ( w_1,w_2,…w_n \right ) $是由各个向量权重组成的，向量$x=\left (x ^{\left ( 1 \right ) } ,x ^{\left ( 2 \right ) },…,x ^{\left ( N \right ) } \right ) $是某个样本数据的特征向量；$b$为偏置常数，则：

$$h\left ( x \right ) =wx+b$$

那么机器学习的任务就是从过去的经验数据中，学习权重系数$w$和偏置常数$b$的最优值，使得回归模型对房子价格预测最准。

2.2 学习策略

    选择合适的策略来学习最优的权重系数$w$和偏置常数$b$。对于回归问题，我们可以使用最小均方误差损失来描述模型的好坏：

$$L\left ( w,b \right ) =\frac{1}{2} \sum_{i=1}^{M}\left [ h\left ( x_{i};w;b \right ) -y_{i} \right ]^{2}$$

其中$ h\left ( x_{i};w;b \right )$是对样本数据$x_{i}$的预测值，$y_{i}$是样本数据$x_{i}$的真实值，样本总数为$M$，$w$是各个特征权重组成的向量，$b$是偏置常数。

当上面的损失函数$L(w,b)$取最小值时，意味着所有样本的预测值和实际值之间的差距是最小的，这时候相当于我们模型的预测效果是最好的。

所以我们的策略就是最小化上面的损失函数：

$$\min_{w,b}L\left ( w,b \right ) =\min_{w} \frac{1}{2} \sum_{i=1}^{M}\left [ h\left ( x_{i};w;b \right ) -y_{i} \right ]^{2}$$

通过求解上面的最优化问题，我们可以得到其中的待定参数$w_j$和偏置常数$b$的值。

2.3 优化算法

    针对上述的优化问题，可以使用常用的梯度下降算法来求解，对损失函数求偏导：

$$\begin{aligned} \frac{\partial }{\partial w}L(w,b) &= \frac{\partial }{\partial w} \left [ \frac{1}{2} \sum_{i=1}^{M} \left [ h\left ( x_i;w;b \right ) -y_i \right ]^2 \right ]\\ &=2\cdot \frac{1}{2}\cdot \left [ h\left ( x_i;w;b \right ) -y_i \right ]\cdot \frac{\partial }{\partial w} \left [ h\left ( x_i;w;b \right ) -y_i \right ]\\ &=\left ( wx_i+b-y_i \right )\cdot \frac{\partial }{\partial w} \left ( wx_i+b-y_i \right )\\ &=\left ( wx_i+b-y_i \right )x_i \end{aligned}$$ $$\begin{aligned} \frac{\partial }{\partial b}L(w,b) &= \frac{\partial }{\partial b}\left [ \frac{1}{2}\sum_{i=1}^{M} \left [ h(x_i;w;b) -y_i \right ]^2 \right ]\\ &=2\cdot \frac{1}{2}\cdot \left [ h(x_i;w;b) -y_i\right ]\cdot \frac{\partial }{\partial b} \left [ h(x_i;w;b) -y_i \right ]\\ &= (wx_i+b-y_i)\cdot \frac{\partial }{\partial b}(wx_i+b-y_i)\\ &= (wx_i+b-y_i) \end{aligned}$$

所以得到权重系数向量$w$和偏置常数$b$的更新公式为：

$$\begin{aligned} w\longleftarrow w-\eta \cdot \frac{\partial }{\partial w}L(w,b) =w-\eta (wx_i+b-y_i)x_i \end{aligned}$$ $$b\longleftarrow b-\eta \cdot \frac{\partial }{\partial b}L(w,b) =b-\eta (wx_i+b-y_i)$$

其中$0< \eta <1$是学习率，这样通过迭代可以使损失函数以较快的速度不断减小，直到满足要求。

3. 算法流程与实现

3.1 算法流程

输入：训练集$T={(x_1,y_1),(x_2,y_2),…,(x_N,y_N)}$，学习率$\eta$。

输出：线性回归模型$h(x)=wx+b$；

步骤如下：

第1步：选取初始向量$w$和偏置常数$b$。

第2步：基于训练集进行参数更新:

$$\begin{aligned} w\longleftarrow w-\eta \cdot \frac{\partial }{\partial w}L(w,b) =w-\eta (wx_i+b-y_i)x_i \end{aligned}$$ $$b\longleftarrow b-\eta \cdot \frac{\partial }{\partial b}L(w,b) =b-\eta (wx_i+b-y_i)$$

第3步：重复步骤2，直至模型满足训练要求。

3.2 算法实现

任务描述：

使用波士顿房价预测，波士顿房价数据与1978年开始统计，共包含506个样本数据点，每个样本都涵盖房屋的13种特征信息和对应的房屋价格，特征情况如下表所示：

特征值	特征说明
ZN	住宅用地所占比例
INDUS	城镇中非商业用地所占比例
NOX	环保指标
RM	每栋住宅的房间数
AGE	1940年以前建成的自住单位比例
RAD	距离高速公路的便利指数
TAX	每一万美元的不动产税率
LSTAT	房东属于低收入阶层的比例
MEDV	自住房屋房价的中位数
…	…

代码实现：

# 1. 数据加载
from sklearn.datasets import load_boston
boston = load_boston()
X = boston.data
y = boston.target
print(X.shape)
print(y.shape)
# 2. 划分数据集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,train_size=0.7)
# 3. 数据标准化
from sklearn import preprocessing
standard_X = preprocessing.StandardScaler()
X_train = standard_X.fit_transform(X_train)
X_test = standard_X.transform(X_test)
standard_y = preprocessing.StandardScaler()
y_train = standard_y.fit_transform(y_train.reshape(-1,1))
y_test = standard_y.transform(y_test.reshape(-1,1))
# 4. 运用ElasticNet回归模型训练和预测
from sklearn.linear_model import ElasticNet
ElasticNet_clf = ElasticNet(alpha=0.1, l1_ratio=0.71)
ElasticNet_clf.fit(X_train, y_train.ravel())
ElasticNet_clf_score = ElasticNet_clf.score(X_test, y_test.ravel())
print('lasso模型得分:', ElasticNet_clf_score)
print('特征权重:',ElasticNet_clf.coef_)
print('偏置值:',ElasticNet_clf.intercept_)
print('迭代次数:', ElasticNet_clf.n_iter_)
# 5. 画图
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(20,3))
axes = fig.add_subplot(1,1,1)
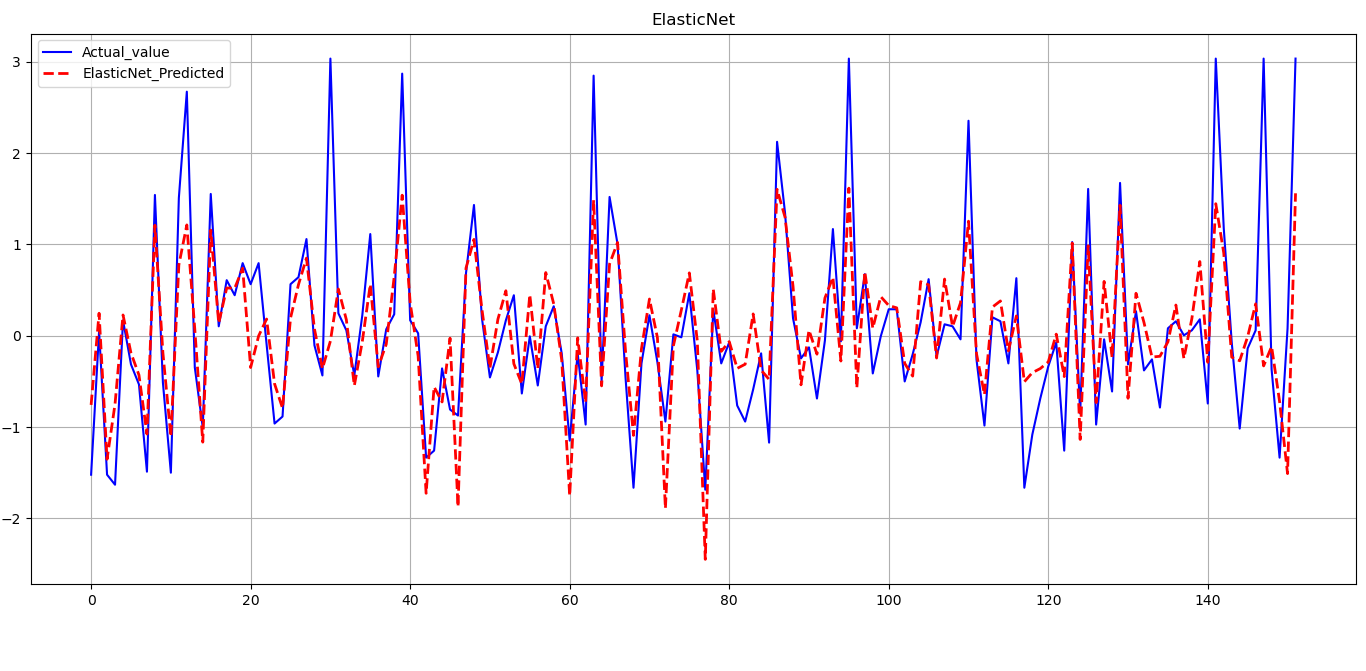
line1, = axes.plot(range(len(y_test)), y_test, 'b', label='Actual_value')
ElasticNet_clf_result = ElasticNet_clf.predict(X_test)
line2, = axes.plot(range(len(ElasticNet_clf_result)), ElasticNet_clf_result, 'r--', label='ElasticNet_Predicted', linewidth = 2)
axes.grid()
fig.tight_layout()
plt.legend(handles=[line1,line2])
plt.title('ElasticNet')
plt.show()

预测结果：