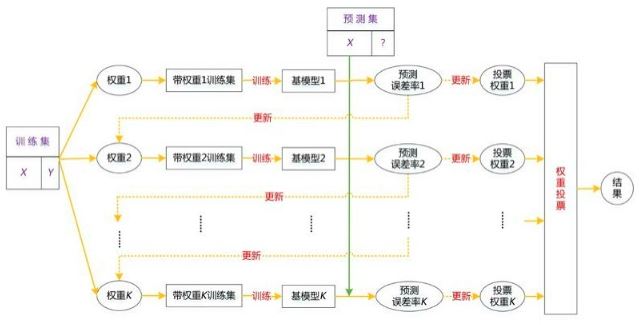
AdaBoost每次训练基模型时都是用所有的训练集样本及样本的所有特征，具体操作过程是：每一轮训练结束后得到一个基学习器，并计算该基学习器在训练样本上的预测误差率，然后根据这个误差率来更新下一轮训练时训练集各样本的权重系数和本轮基学习器的投票权重，目标是使得本轮被错误预测了的样本在下一轮训练中得到更大的权重，使其受到更多的重视，并且预测越准确的基学习器在最后集成时占的投票权重系数越大。这样通过多轮迭代可以得到多个基学习器及其对应的投票权重，最后按照各自的权重进行投票来输出最终的预测结果。如图所示：

1 AdaBoost的工作过程

AdaBoost的运行主要涉及4个问题：

问题1：如何计算每一次训练集样本的权重?

AdaBoost每一轮都会使用全部的训练集样本，但是每一轮都会改变样本的权重分布，其方法是：用本轮得到的基学习器对所有训练样本进行一次预测，得到一个预测误差率；下一轮训练中各个训练样本的情况由该训练样本自身、本轮基学习器对该样本的预测值、本轮基学习器对训练样本的整体预测误差率三者共同决定。

问题2：如何训练基模型？

AdaBoost与RF一样，既可以用于分类也可以用于回归问题，因为它们默认使用的基学习器都是CART决策树。所以，只要每一轮将原始样本按照新的权重系数重新计算出来后，基学习器的训练与普通的单模型训练过程是完全一致的。

问题3：如何计算基模型的预测误差率？

对于分类问题，计算模型的预测误差率可以直接使用0-1损失函数；对于回归问题，计算模型的预测误差率可以使用平方损失函数或指数损失函数。

问题4：如何计算各个基学习器的投票权重？

各个基学习器的投票权重$\alpha_k$是根据每一轮的预测误差率计算得到的，假设通过K轮迭代，我们得到了各个基学习器的投票权重$\alpha_k,k=1,2,…,K$，那么对于结果为{1,-1}的二分类问题，最后的投票公式是：

$f(x)=sign\sum_{k=1}^{K} \alpha _k\cdot T_k(x) \tag{1.1}$

其中，$T_k(x)$是第k个基学习器的预测结果值。

2 AdaBoost多分类问题

AdaBoost多分类问题有两种实现算法，分别称作SAMME算法和SAMME.R算法。两个算法的主要思想一致，只不过在分类过程中，某些步骤采用了不同的处理方式。

对于包含有M个样本的训练集$T=\left \{ (x_1,y_1),(x_2,y_2),…,(x_M,y_M) \right \} $，假设样本总共有L个类别，即$y_i\in \left \{ c_1,c_2,…,c_L \right \},i=1,2,…,M $,AdaBoost多分类问题的处理过程如下：

2.1 SAMME算法

第1步：初始化数据的分布权重，采用平等对待的方式，即：

$D_1=(w_{11},w_{12},...,w_{1M}),w_{1i}=\frac{1}{M},i=1,2,...,M \tag{2.1}$

第2步：利用具有权重$D_1$的训练数据集，采用某个基本模型进行训练，得到第一个基分类器$T_1(x)$。

第3步：计算基分类器$T_1(x)$在训练集上的分类误差率$e_1$，即：

$e_1=\sum_{i=1}^{M}w_{1i}I(T_1(x_i)\ne y_i) \tag{2.2}$

第4步：按照下式计算基分类器$T_1(x)$的投票权重$\alpha_1$。

$\alpha _1=\frac{1}{2}ln\frac{1-e_1}{e_1}+ln(L-1) \tag{2.3}$

这里的$L$是多分类的类别数，当$L=2$时，相当于二分类问题。

按照公式(2.3)来取值，当分类误差率$e_1<\frac{1}{2}$时，一方面可以保证基分类器的投票权重$\alpha_1>0$；另一方面，可以保证基分类器的投票权重$\alpha_1$随着$e_1$的减小而增加。这样产生的效果是：当基分类器的分类误差率小于0.5时，分类器的分类误差率越小，最终它获得的投票权重就越大，从而自动让最终的模型偏向于预测效果较好的基学习器，这是AdaBoost的第一个巧妙之处。

第5步：按下式更新第二轮训练集的权重分布。

$D_2=(w_{21},w_{22},...,w_{2M}) \tag{2.4}$

其中：

$w_{2i}=\frac{w_{1i}exp(-\alpha _1y_iT_i(x_i))}{\sum_{i=1}^{M}w_{1i}exp(-\alpha _1y_iT_1(x_i)) } ,i=1,2,...,M$

上式的分母可以看做是一个归一化因子，将其记为:$Z_k,k=1,,2,…,K$，下表k表示的是第k轮，则：

$w_{2i}=\frac{w_{1i}exp(-\alpha _1y_iT_i(x_i))}{Z_2} ,i=1,2,...,M$

又因为$y_i\in\left \{ -1,1 \right \} (i=1,2,…,M)$是样本$x_i$的实际值，$G_1(x_i)$是样本$x_i$的预测值，即$\in\left \{ -1,1 \right \} $，所以上式可等价写成:

$w_{2i}=\begin{cases} \frac{w_{1i}}{Z_2}e^{-\alpha _1} ,T_1(x_i)=y_i \\ \frac{w_{1i}}{Z_2}e^{\alpha _1},T_1(x_i)\ne y_i \end{cases}\tag{2.5}$

$\alpha_1$是第一轮训练的基分类器的投票权重，它的值大于0的，所以上面的式子其实反映的是：当$T_1(x_i) \ne y_i$时，在下一轮训练中，其对应的样本权重$w_{2i}$会在$w_{1i}$的基础上变大，而当$T_1(x_i)=y_i$时，在下一轮训练中，其对应的样本权重$w_{2i}$会在$w_{1i}$的基础上缩小。

这样导致的一个效果就是，上一轮被错误分类了的样本，在这一轮中，其对应的样本权重会被放大；而上一轮被正确分类了的样本，在这一轮中，其对应的样本权重会被缩小。随着基学习器的一轮轮迭代，AdaBoost会越来越把注意力集中到之前分类错误的样本上。这就是AdaBoost的第二个巧妙之处。

第6步：利用更新后得到的第2轮的样本权重再次训练得到第2个基分类器$T_2(x)$，由$T_2(x)$计算分类误差率$e_2$和投票权重$\alpha_2$，最终重复上述过程多次，总共可得到K个基分类器$T_1(x),T_2(2),…,T_k(x)$及其对应的投票权重$\alpha_1,\alpha_2,…,\alpha_k$，然后按照下式做集成：

$f(x)=arg\max_{c_i}\left [ \sum_{k=1}^{K} \alpha _kI(T_k(x)=c_i) \right ] \tag{2.6}$

上式表示让每个基分类器$T_k(x),(k=1,2,…,K)$对样本x进行一次带权投票，最后选出得票分数最大的类别$c_i$作为样本$x$的最终预测类别。这里$I$取所有$L$个类别$c_1,c_2,…,c_L$中的一个。实际上，当为二分类问题时，上式就等价于下面的形式：

$f(x)=sign(\sum_{k=1}^{K}\alpha _kT_k(x) ) \tag{2.7}$

2.2 SAMME.R算法

第1步：先初始化数据的分布权重，采用平等对待的方式，即：

$D_1=(w_{11},w_{12},...,w_{1M}),w_{1i}=\frac{1}{M,i=1,2,...,M}\tag{2.8}$

第2步：利用具有权重$D_1$的训练数据集，采用某个基本模型（可以是适合训练集数据类型的任意模型）进行训练，得到第一个基分类器$T_1(x)$。

第3步：利用，基分类器$T_1(x)$计算各训练集样本$x_i$属于各类别$c_m$的加权概率，即：

$p_{1i}^{l}=w_{1i}P(y_i=c_l|x_i),i=1,2,...,M,l=1,2,...,L \tag{2.9}$

第4步：计算基分类器$T_1(x)$对样本$x_i$在第$l$个类别上的投票权重。

$a_1^{(l)}(x_i)=(L-1)(lnp_{1i}^{(l)}-\frac{1}{L}\sum_{l=1}^{L}lnp_{1i}^{(l)}),l=1,2,...,L \tag{2.10}$

第5步：按照下式更新第二轮训练集的权重分布。

$D_2=(w_{21},w_{22},...,w_{2M})\tag{2.11}$

其中:

$w_{2i}=w_{1i}\cdot exp(-\frac{L-1}{L}\sum_{l=1}^{L}\delta _i^{(l)}lnp_{1i}^{(l)} ),i=1,2,...,M \tag{2.12}$ $\delta _i^{(l)}=\left\{\begin{matrix} 1,y_i=c_l\\ -\frac{1}{L-1},y_i\ne c_l \end{matrix}\right. \tag{2.13}$

第6步：归一化训练集样本权重$D_2=(w_{21},w_{22},…,w_{2M})$，使得权重之和为1.

第7步：利用更新后得到的第2轮的样本权重再次训练第2个基分类器$T_2(x)$；由$T_2(x)$计算$p_{2i}^{(l)}$和$a_2^{(l)}(x_i)$，得到$D_3$；重复此过程，直到得到最终$K$个基分类器及$K$个基分类器所对应的$a_k^{(l)}(x_i),k=1,2,…,K,l=1,2,…,L$，并按照下式进行组合得到最终的多分类器：

$f(x)=arg\max_{c_l}[\sum_{k=1}^{K}a_k^{(l)}(x_i) ] \tag{2.14}$

3 AdaBoost的回归问题

AdaBoost的回归问题与分类问题的过程及原理类似，只是在计算预测误差率时采用的方式不同，分类问题采用的是0-1损失，而回归问题一般采用平方和或指数误差来衡量误差率。进行基学习器集成时，分类问题采用的是按权重投票决定最终结果，而回归问题是取各基学习器预测结果乘以各自权重后的求和作为最终结果。

AdaBoost回归问题的处理过程如下：

输入：训练集$T=\left \{ (x_1,y_1),(x_2,y_2),…,(x_M,y_M) \right \} $。

输出：最终的集成模型$f(x)$。

步骤如下：

第1步：先初始化数据的分布权重，采用平等对待的方式，即：

$D_1=(w_{11},w_{12},...,w_{1M}),w_{1i}=\frac{1}{M,i=1,2,...,M}\tag{2.15}$

第2步：利用具有权重$D_1$的训练数据集，采用某个基本模型（可以是适合训练集数据类型的任意模型）进行训练，得到第一个基分类器$T_1(x)$。

第3步：计算基分类器$T_1(x)$在训练集上的预测误差率$e_1$。

(a)先计算训练集上的最大误差:$E_1=max|y_i-T_1(x_i)|$

(b)再计算每个样本的相对误差$e_{1i},i=1,2,…,M$

(c)计算回归预测误差率:$e_1=\sum_{i=1}^{M}w_{1i}e_{1i} $

第4步：按下式计算基分类器$T_1(x)$的投票权重$\alpha_1$。

$\alpha_1=\frac{e_1}{1-e_1} \tag{2.16}$

第5步：按下式更新第二轮训练集的权重分布：

$D_2=(w_{21},w_{22},...,w_{2M})\tag{2.17}$

第6步：利用更新后得到的第2轮的样本权重再次训练一个基学习器，重复上述过程K次，得到K个基学习器$T_1(x),…,T_k(x)$及其对应的权重$\alpha_1,…,\alpha_k$，最后按照下式做集成：

$f(x)=\sum_{k=1}^{K}(ln\frac{1}{\alpha _k} )T_k(x) \tag{2.18}$

4 总结

AdaBoost的优点：

(1) 基学习器可以有多种选择，构建比较灵活。

(2) AdaBoost作为分了器时，分类精度较高，而且不容易发生过拟合。

缺点：

(1) AdaBoost对噪声比较敏感，因为异常样本在迭代中很可能会获得较高的权重。